El Diagrama de Árbol en el cálculo de probabilidades

Un Diagrama de Árbol es una herramienta que se utiliza para determinar todos los posibles resultados de un experimento aleatorio. En el cálculo de muchas probabilidades se requiere conocer el número de objetos que forman parte del espacio muestral, estos se pueden determinar con la construcción de un diagrama de árbol.

Para la construcción de un diagrama en árbol se partirá poniendo una rama para cada una de las posibilidades, acompañada de su probabilidad. Cada una de estas ramas se conoce como rama de primera generación.

En el final de cada rama de primera generación se constituye a su vez, un nudo del cual parten nuevas ramas conocidas como ramas de segunda generación, según las posibilidades del siguiente paso, salvo si el nudo representa un posible final del experimento (nudo final).

Hay que tener en cuenta que la construcción de un árbol no depende de tener el mismo número de ramas de segunda generación que salen de cada rama de primera generación y, lo que es más importante, que la suma de probabilidades de las ramas de cada nudo ha de valer 1.

Existe un principio sencillo de los diagramas de árbol que hace que éstos sean mucho más útiles para los cálculos rápidos de probabilidad:

Por ejemplo, multiplicamos las probabilidades si se trata de ramas adyacentes (contiguas), o bien las sumamos si se trata de ramas separadas que emergen de un mismo punto. Ejemplo:

Una universidad está formada por tres facultades:
La 1ª con el 50% de estudiantes.
La 2ª con el 25% de estudiantes.
La 3ª con el 25% de estudiantes.

Las mujeres están repartidas uniformemente, siendo un 60% del total en cada facultad.

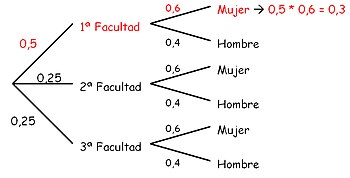
Construimos el diagrama de árbol, partiendo de la primera información que tenemos: las facultades que forman la universidad y de cada una de las facultades saldrán don ramas para indicar el porcentaje de mujeres y hombres, colocando encima de cada rama su probabilidad y comprobando que su suma sea la unidad.

Cómo resolveríamos la siguiente cuestión: ¿Cuál es la probabilidad de encontrar una alumna de la primera facultad?

Multiplicando las ramas de 1ª facultad y que sea mujer, tendremos:

P(alumna de la 1a facultad) = 0,5⋅0,6 = 0,3

Y, cómo resolveríamos ahora esta cuestión: ¿Cuál es la probabilidad de encontrar un alumno varón?

Multiplicando las probabilidades de las ramas de 1ª facultad y que sea hombre, mas la multiplicación de las probabilidades de las ramas de 2ª facultad y que sea hombre y también habrá que sumarle la probabilidad de multiplicar las probabilidades de las ramas de la 3ª facultad y que sea hombre, por lo que tendremos:

P(sea hombre) = 0,5·0,4 + 0,25·0,4 + 0,25·0,4 = 0,4

A continuación, les dejo tres videos explicativos donde se aplica, en diferentes problemas, la construcción de un diagrama de árbol. 

Aconsejo que, ante los problemas que platean en los videos, intentes resolverlos tú previamente, copiándolos en una hoja, intentando construir tu diagrama de árbol y comprobarlo con el que plantea el video. Saben bien, que si no lo intento... no lo consigo.